Open Library - открытая библиотека учебной информации. Обнаженное обдуваемое ветром дерево пифагора Используя рекурсивную процедуру построить фигуру дерево пифагора

Дерево Пифагора - один из видов фрактала, который основан на фигуре, известной под именем «Пифагоровы штаны».

Доказывая свою знаменитую теорему, Пифагор построил фигуру, в которой на каждой стороне прямоугольного треугольника были расположены квадраты. Спустя время эта фигура Пифагора превратилась в целое дерево. Первым дерево Пифагора построил в период второй мировой войны А. Босман, пользуясь обычной чертежной линейкой.

Одним из основных свойств дерева Пифагора считается то, что когда площадь первого квадрата составляет единицу, то на каждом из уровней сумма площадей квадратов также будет равна единице. Классическое дерево Пифагора имеет угол, равный 45 градусам, но также можно построить обобщённое дерево Пифагора, используя другие углы. Такое дерево называют обдуваемым ветром деревом Пифагора. Если изобразить только отрезки, которые соединяют каким-либо образом определенные «центры» треугольников, тогда получится обнаженное дерево Пифагора.

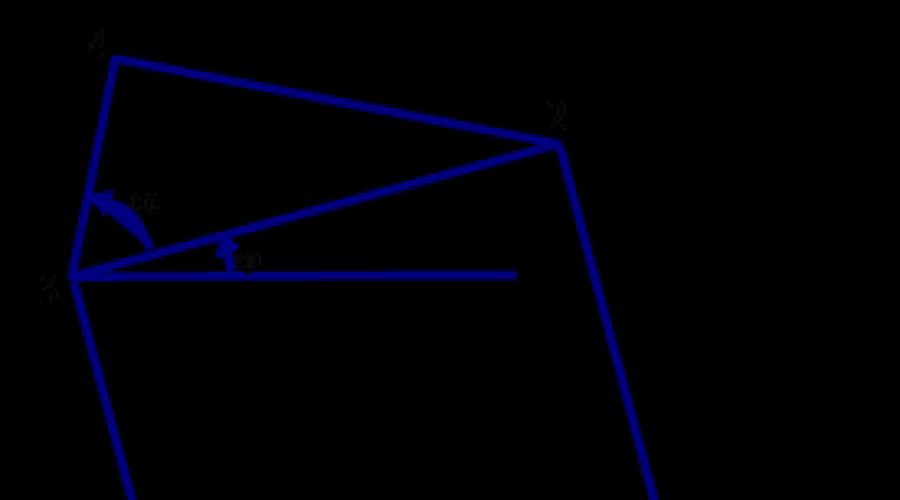
Следующим примером может быть известное "Пифагорово дерево". Оно часто изображается так, как показано на рис. 3.2. Каждый из прямоугольных треугольников в этом дереве имеет внутренний угол, равный 45°.

Опять воспользуемся генератором случайных чисел для создания более общей программы, которая может сформировать не только рис. 3.2, но также генерировать и менее регулярные деревья. Углы, задаваемые равными 45° для рис. 3.2, в общем случае будут задаваться случайным образом в пределах между (45 - delta) ° и (45 + delta) °, где значение delta задается в качестве входного параметра вместе с параметром n, определяющим глубину рекурсии. Регулярная версия, изображенная на рис. 3.2, получается при задании delta = 0 и n = 7. На рисунке параметр п определяет количество треугольников на пути от корня до листьев дерева. Сердцевиной программы будет рекурсивная функция square_and_triangle ("квадрат и треугольник") с параметром n, определяющим глубину рекурсии, в качестве первого аргумента. Если значение параметра n больше нуля, то задачей функции square_and_triangle, как это определяется названием, будет вычертить квадрат и над ним треугольник, а затем еще дважды обратиться к самой себе с соответствующими новыми аргументами, первый из которых задается равным n-1. Размер и положение квадрата полностью определяются четырьмя параметрами: X0,Y0, а и j (см. рис. 3.3). Для вычерчивания треугольника необходимо знать угол a. Этот угол, выраженный в градусах, равен 45+deviation , где deviation равно одному из целых чисел ряда -delta, -delta+I, ... , delta, выбираемому случайным образом. На рис. 3.3 необходимые точки пронумерованы последовательными числами 0,1,2,3,4. Координаты X0 , Y0 точки О задаются в обращении к функции. Для вычисления остальных точек вначале рассмотрим более простую ситуацию при j = 0 , то есть когда сторона 0 1 квадрата занимает горизонтальное положение.

В этом положении координаты точек определить очень просто. Они записываются в массивах х и у. Затем вся конструкция поворачивается вокруг точки О на угол j. Результат поворота записывается в массивах хх и уу.

/* PYTH_TREE: Вариант дерева Пифагора */

#include "math.h"

#include "stdlib.h"

#include "time.h"

#define pi 3.1415927

#include "stdio.h"

struct {float xx; float yy; int ii;} s;

void pfopen(){ fp=fopen("scratch", "wb"); }

void pmove(float x,float y)

{ s.xx=x; s.yy=y; s.ii=0; /* 0 = pen up */ /* 0 = перо поднято */

fwrite(&s, sizeof s, 1, fp);

void pdraw(float x,float y)

{ s.xx=x; s.yy=y; s.ii=1; /* 1 = pen down */ /* 1 = перо опущено */

fwrite(&s, sizeof s, 1, fp);

void pfclose(){ fclose(fp); }

void square_and_triangle(int n,float x0,float y0, float a, float phi)

{ float x, y, xx, yy, cphi, sphi, c1, c2, b, c,

alpha, calpha, salpha;

int i, deviation; /* phi and alpha in radians */

/* delta in degrees */

if(n==0) return; /* углы phi и alpha в радианах */

/* угол delta в градусах */

deviation=rand()%(2*delta+1)-delta;

alpha=(45+deviation)*pi/180.0;

x=x=x0; x=x=x0+a;

y=y=y0; y=y=y0+a;

calpha=cos(alpha); salpha=sin(alpha);

c=a*calpha; b=a*salpha;

/* Rotation about (x0, y0) through angle phi ; */

/* Поворот вокруг точки (x0, y0) на угол phi;*/

cphi=cos(phi); sphi=sin(phi);

c1=x0-x0*cphi+y0*sphi;

c2=y0-x0*sphi-y0*cphi;

for (i=0; i<5; i++)

{ xx[i]=x[i]*cphi-y[i]*sphi+c1;

yy[i]=x[i]*sphi+y[i]*cphi+c2;

for (i=0; i<5; i++) pdraw(xx[i],yy[i]);

square_and_triangle(n-1, xx, yy, c, phi+alpha);

square_and_triangle(n-1, xx, yy, b, phi+alpha-0.5*pi);

pfopen(); time(&seed); srand((int)seed);

printf (" Задайте угол delta в градусах (0 < delta < 45) ");

scanf("%d", &delta);

printf(" Задайте глубину рекурсии n "); scanf("%d", &n);

square_and_triangle(n, 0.0, 0.0, 1.0, 0.0);

Эта программа формирует файл SCRATCH, который должен быть обработан программой GENPLOT из лекции 2. Графический результат работы программы для delta = 30 и п = 7 показан на рис. 3.4.

Дерево Пифагора - один из видов фрактала, который основан на фигуре, известной под именем «Пифагоровы штаны».

Доказывая свою знаменитую теорему, Пифагор построил фигуру, в которой на каждой стороне прямоугольного треугольника были расположены квадраты. Спустя время эта фигура Пифагора превратилась в целое дерево. Первым дерево Пифагора построил в период второй мировой войны А. Босман, пользуясь обычной чертежной линейкой.

Одним из основных свойств дерева Пифагора считается то, что когда площадь первого квадрата составляет единицу, то на каждом из уровней сумма площадей квадратов также будет равна единице. Классическое дерево Пифагора имеет угол, равный 45 градусам, но также можно построить обобщённое дерево Пифагора, используя другие углы. Такое дерево называют обдуваемым ветром деревом Пифагора. Если изобразить только отрезки, которые соединяют каким-либо образом определенные «центры» треугольников, тогда получится обнаженное дерево Пифагора.

Множество Мандельброта классический образец фрактала … Википедия

HTML HTML и HTML5 Динамический HTML … Википедия

Множество Мандельброта классический образец фрактала Фрактал (лат. fractus дробленый) термин, означающий геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре… … Википедия

Кривая Леви фрактал. Предложен французским математиком П. Леви. Получается, если взять половину квадрата вида /, а затем каждую сторону заменить таким же фрагментом, и, повторяя эту операцию, в … Википедия

Бассейны Ньютона … Википедия

Граф Кэли граф, который строится по группе с выделенной системой образующих. Назван в честь Кэли. Определение Пусть дана дискретная группа G и система образующих S. Предположим S = S − 1, то есть, для каждого. Графом Кэли группы G по системе… … Википедия

Граф, который строится по группе с выделенной системой образующих. Назван в честь Кэли. Определение Пусть дана дискретная группа и система образующих. Предположим, то есть, для каждого. Графом Кэли группы … Википедия

Древнеиранская религия в античных источниках. Статья содержит обзор сведений античных авторов (древнегреческих, латинских и отчасти армянских и сирийских) V века до н. э. VI века н. э. о религии иранских народов эпохи Ахеменидов, парфян и державы … Википедия

Культура народов, населявших в древности, в 4 1 м тыс. до н. э., Месопотамию Двуречье Тигра и Евфрата (территория современного Ирака), шумеров и аккадцев, вавилонян и ассирийцев, создавших крупные государства Шумер, Аккад, Вавилонию (См.… … Большая советская энциклопедия

Книги

• На излете лета , Вера Орловская. Новая книга Веры Орловской НА ИЗЛЕТЕ ЛЕТА продолжает удивлять читателя разнообразием форм и тем, о чем говорят и некоторые названия: ФИЛОСОФИЯ ПИФАГОРА В ЧИСЛАХ, ДЕРЕВО СНА, СИМФОНИЯ № 1…
• R-функции как аппарат в приложениях фрактальной геометрии , А. В. Толок. Математический аппарат теории R-функций применяется для описания объектов фрактальной геометрии функциями ɷ(x) = 0, x ∈ Еn , где ɷ(x) имеет вид единого аналитического выражения. Авторами…

Привет, друзья, интересующиеся фракталами и не только. Начиная с этого момента, я запускаю серию постов, в которых буду объяснять принципы построения простейших фракталов. Изучать всегда интересно и я помогу вам в этом: отныне мы будем знать многие и многие фракталы. Аттрактор Лоренца в статье про хаос был тому примером. А сегодня я расскажу вам про дерево Пифагора.

Итак, что это такое? Дерево Пифагора – это простейший фрактал, который можно начертить на бумаге. Но почему этот фрактал называется деревом Пифагора? Дело в том, что здесь есть связь с теоремой Пифагора – одной из основ евклидовой геометрии. Помните ее? Я напомню: а2 + b2 = c2 (сумма квадратов длин катетов равна квадрату длины гипотенузы). Эта теорема известна с древности, доказательств теоремы в настоящее время насчитывают более 400, и только Пифагор впервые доказал ее геометрически. Он построил такую фигуру: взял прямоугольный треугольник и на его сторонах нарисовал квадраты. Такая фигура еще называется «Пифагоровы штаны»:

Если продолжить данную конструкцию рекурсивно, то мы получаем в итоге дерево Пифагора:
1 итерация (в нашем дереве Пифагора угол равен 45 градусам):

Вторая итерация:

Третья итерация:

Десятая итерация:

Важное свойство дерева Пифагора: если площадь первого квадрата равна единице, то на каждом уровне сумма площадей квадратов тоже будет равна единице.
Если угол изменить с 45 градусов, то можно построить и другие типы дерева Пифагора.
Вот, к примеру, так называемое «обдуваемое ветром дерево Пифагора»:

В некоторых генераторах фрактальной графики реализована формула построения фрактала на основе дерева Пифагора. Эта реализация очень напоминает IFS – системы, особенно если заменить квадраты на прямоугольники или вытянутые фигуры.
На сегодня всё, до следующих встреч, в которых будет много других интересных фракталов)